[이데일리 이연호 기자] “EH FDUHIXO IRU DVVDVVLQDWRU”
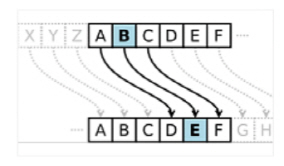
위 문장이 무슨 뜻인지 알겠는가. 고대 로마제국의 정치가이자 군인이었던 율리우스 카이사르가 썼던 암호다. 하나의 힌트를 준다. 힌트는 -3이다. 바로 위 문장은 ‘BE CAREFUL FOR ASSASSINATOR(암살자를 조심하라)’는 뜻이다. 카이사르는 이 내용(평문)을 전달하기 위해 평행이동이라는 방법을 사용했다. 평문은 암호문(EH FDUHIXO IRU DVVDVVLQDWRU)에서 사용된 알파벳 각각을 암호 키(key)인 -3(개)만큼 평행 이동하면 비로소 완성된다. 즉 알파벳 순서상 E보다 3개 앞의 알파벳은 B가 되고 마찬가지로 H는 E가 되는 식이다. 암호문 속 E가 암호키 -3을 만나 B가 되는 과정을 암호화 알고리즘이라고 할 수 있다. 약 2500년 전 스파르타 시대부터 시작된 것으로 알려진 암호의 역사는 기밀 유지를 요하는 각종 크고 작은 전쟁에서 가장 활발하게 사용돼 왔다.
|
앞에서 본 카이사르 암호는 암호화와 복호화(암호 해독) 시 동일한 키인 -3 을 사용하는 대칭키 알고리즘이다. 다만 대칭키 알고리즘은 ‘키 배송’이라는 결정적 문제가 존재한다.
송신자는 수신자에게 암호 키를 전달해야만 하는데 이 키가 배송 과정에서 노출되면 아무리 뛰어난 암호화 알고리즘을 사용했더라도 평문이 공개돼 버리기 때문이다. 바로 이 키 배송 문제를 해결하기 위해 나온 방식이 비대칭키(공개키) 알고리즘이다.
공개키 암호 알고리즘은 암호화와 복호화 시 서로 다른 두 키를 사용한다. RSA 는 대표적인 공개키 암호 알고리즘으로 현재 공개 키 암호 체계에서 중요한 표준 중 하나다. 큰 수의 소인수 분해 과정이 어렵다는 점에 기반한 알고리즘이다. 큰 수의 소인수 분해 과정은 많은 시간이 걸리지만 소인수 분해된 두 소수(1과 자기 자신만으로 나눠 떨어지는 1보다 큰 양의 정수)를 알면 원래의 큰 수는 곱셈에 의해 간단히 구해 낼 수 있다. 4529524369라는 숫자는 두 소수의 곱으로 이뤄진 합성수(자연수에서 1과 소수를 제외한 나머지 수)다. 이 합성수를 m이라고 하면 이 m이 어떤 두 수(n1, n2)의 곱으로 이뤄졌는지 빠르게 알아낼 수 있을까? 두 수의 답은 n1=48611과 n2=93179라는 소수다. 두 소수의 곱 m을 알더라도 n1과 n2가 무엇인지 알기 어려운 것이 RSA가 가진 보안성이라고 이해하면 쉽다. RSA는 위의 두 소수를 이용해 특정한 개인만 알 수 있는 개인키(Private Key)와 모두가 알 수 있는 공개키(Public Key)라는 두 개의 키를 쌍으로 만들어 사용한다. 공개키 암호 알고리즘은 금융 거래 등에 활발하게 사용되는 공인인증서에서도 사용하고 있다. 공개키가 계좌번호, 개인키가 비밀번호라고 생각하면 이해하기 쉽다.
|
도움말=민무홍 과학커뮤니케이터(고려사이버대 정보관리보안학과 외래교수).